¿QUE ES UNA FUNCION?
Una función f es una relacion donde todos los elemntos x .El conjunto de partida tiene una sola imagen f(x) en el conjunto de llegada . La expresion f(x) es el valor de f ubicado con x y se lee "f de x"
ELEMENTOS DE UNA FUNCIÓN
Dominio:
Al conjunto de partida se le llama dominio y es el conjunto de los valores sobre los que se aplica la función.
Rango:
Son el conjunto de las imágenes de algunos elementos del conjunto de partida.
Condominio:
Al conjunto de llegada se le llama codominio y es el conjunto de las posibles imágenes de los elementos del conjunto de partida.
TIPOS DE FUNCIONES.
POLINOMIAL:
Estas funciones son modelos que describen relaciones entre dos variables que intervienen en diversos problemas del mundo real.
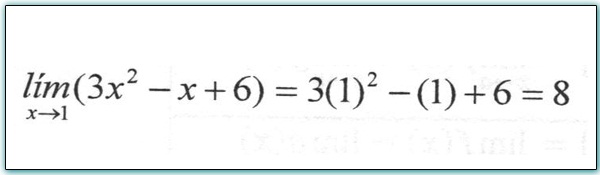
Alguna propiedades de las funciones polinomiales
1. La gráfica de y = f (x) intercepta al eje Y en el punto (0,c)
2. La gráfica de y = f (x) intercepta al eje X en los puntos cuyas abscisas son las raíces de la
ecuación a xn + + a1x + a0 = 0
3. Las funciones polinomiales son funciones continuas.
*Para hacer la grafica de una funcion polinomica, se debe determinar los puntos de interccecion, con el eje "x" que se obtiene haciendo "y=0"
Entre las funciones polinomiales se encuentran por ejemplo: las funciones constantes, las
funciones lineales, las funciones cuadráticas, las funciones cúbicas
A) FUNCIÓN CONSTANTE
Una función constante es aquella que tiene la forma y=f(x)=c, donde c es un número real fijo.
El dominio de una función constante es IR, y su recorrido es {c}. Su gráfica es una rectaparalela (o coincidente) al eje X.
FUNCION RACIONAL:
Son funciones compuestas por dos polinomios, y esta definida para todos los reales
F(x)=p(x)/q(x)
en estas funcione el denominador siempre tiene que se diferente de cero en este caso seria.
q(x)diferentes a 0
EJEMPLO:
FUNCION LINEAL.
Todas las funciones que representan una recta en el plano cartesiano, resiven el nombre de funciones lineales o de primer grado. Las funciones linea les se formulan mediante ecuaciones de primer grado.
EJEMPLO:
 |
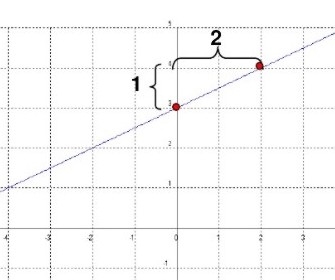F(X)=mx+b donde m es la pendiente y b es el termino independiente que corresponde al corte de la recta con el eje "y" (eje de las cordenadas) como podemos observar en la grafica.
funcion cuadratica.
las funciones cuadraticas, tambien conocidas como funciones de sengundo grado. Estas funciones se caracterizan por tener la variable independiente al cuadrado, y su grafica se denomina parabola. La ecuacion general que la define es:
donde A, B, C son nuemero reales, con:
GRAFICA:
una parabola es un conjunto de puntos en un plano que es paralelo de un punto fijo y de una linea fija llamadas foco (f) y directriz respectivamente.
EJEMPLO:
FUNCION IRRACIONAL.
Una funcion es irracional si aparece una expresion algebraica que contenga a x
dentro de un radical:
donde g(x) es una expresion algebraica que contiene a x.
Su grafica seria:
EJEMPLO:
FUNCIONES COMPUESTAS.
Dadas dos funciones f(x) y g(x), se llama función compuesta de f con g, y escribimos g o f, a aquella función en la que la imagen de un número real x es el resultado de actuar sucesivamente sobre x primero f y después g. |
Propiedades de la composición
ASOCIATIVA: Dadas tres funciones cualesquiera f(x), g(x) y h(x) se cumple que ho(gof) = (hog)of.
CONMUTATIVA: La composición de funciones en general no es conmutativa, es decir, gof y fog son en general dos funciones distintas.
En el ejemplo anterior (gof)(x) =6x + 1, sin embargo, (fog)(x) = f[g(x)] = f(2x + 5) = 3(2x + 5) - 2 = 6x + 15 - 2 = 6x + 13, luego las funciones gof y fog son distintas.
FUNCIÓN IDENTIDAD: La función i(x) = a que hace corresponder a cada número real con él mismo, al componerla con cualquier función f(x) da de resultado f(x). Además i(x) conmuta con todas las funciones, por tanto i(x) es el elemento neutro de la composición de funciones.
funciones pares e impares.
Se dice que una función es par si f(x) = f(-x), en el caso de que f(x) = -f(-x) se dice que la función es impar.
Ejemplos 1:
La función y(x)=x es impar ya que:
f(-x) = -x
Pero como f(x) = x entonces:
f(-x) = - f(x).
FUNCIONES BIYECTIVAS E INYECTIVAS.
Una función es inyectiva si cada f(x) en el recorrido es la imagen de exactamente un único elemento del dominio. En otras palabras, de todos los pares (x,y) pertenecientes a la función, las y no se repiten.
Para determinar si una función es inyectiva, graficamos la función por medio de una tabla de pares ordenados. Luego trazamos líneas horizontales para determinar si las y (las ordenadas) se repiten o no.
EJEMPLO A: Determinar si la siguiente función es o no inyectiva: f(x) = x2 – 2 |
Primero elaboramos una tabla de pares ordenados y luego graficamos.
|
x |
–2 |
–1 |
0 |
1 |
2 |
|
f(x) |
2 |
–1 |
–2 |
–1 |
2 |
vemos que nuestra lineas horizontales rojas cortan la funcion en mas de un punto esto indica que las "y" se repiten por lo tanto f(x) no es inyectiva.
Función biyectiva
Ejemplo de función biyectiva.
En matemática, una función es biyectiva si es al mismo tiempo inyectiva y sobreyectiva.
Formalmente,
para ser más claro se dice que una función es biyectiva cuando todos los elementos del conjunto de partida en este caso (x) tienen una imagen distinta en el conjunto de llegada, que es la regla de la función inyectiva. sumándole que cada elemento del conjunto de salida le corresponde un elemento del conjunto de llegada, en este caso (y) que es la norma que exige la función sobreyectiva
FUNCIONES TRIGONOMETRICAS:
Las funciones trigonométricas surgen de una forma natural al estudiar el triángulo rectángulo y observar que las razones entre ellas longitudes de los cualesquiera de sus lados solo depende del valor de los ángulos del triángulo.Existen seis clases de funciones trigonométricas: seno y su inversa, la cosecante; coseno y su inversa, la secante; y tangente y su inversa, la cotangente. Para cada una de ellas pueden también definirse funciones circulares inversade las funciones trigonometricas:
Funcion del seno:
Se denomina funcion del seno y se denota por f (x) 5 sen x, a la aplicación de la razón trigonométrica seno a una variable independiente x expresada en radianes. La función seno es periódica, acotada y continua, y su dominio de definición es el conjunto de todos los números reales.
Gráfica de la función seno.
FUNCION EXPONENCIAL :
Se llama funcion exponencial de base a aquella cuya forma genérica es f (x) = ax, siendo a un número positivo distinto de 1. Por su propia definición, toda función exponencial tiene por dominio de definición el conjunto de los números reales R.
La función exponencial puede considerarse como la inversa de la función logarítmica, por cuanto se cumple que:
BIBLIOGRAFIA Y CIBERGRAFIA :
-Formula de undecimo grado,guia del educador/Diego Fernando Pulecio Herrera.Editado por: Victor Hernando Ardila Gutierrez
-https://www.vitutor.com/fun/2/c_1.html
Fotogalería: Inicio
La galería de imágenes está vacía.